Sponsored by:




Curve Shape in Digital Photography
(Why a Linear Curve May Not Be Straight, And Other Curiosities)
Contents:
* Introduction
* The eye's response to light is logarithmic.
* In film photography, we always use logarithmic scales.
* The computer screen's response to pixel values is close to antilogarithmic.
* In Photoshop, the tone curves represent pixel values.
* The digital sensor's response to light is linear.
* Digital cameras normally convert sensor values to appropriate screen pixel values.
* For dark frame subtraction and other kinds of analysis, we need linear conversion.
Introduction
Curve shape is the difference between these three pictures:



It would not be correct to say that they differ in darkness or lightness,
because all three have the same maximum white and minimum black.
They differ only in the position of the midtones relative to the highlights and shadows.
This is what it would look like if they differed in brightness
and not curve shape:



Here one is too dark (with no whites) and one is too light (with no blacks).
See the difference?
In what follows, my goal is to explain curve shape as it applies to digital photography.
I haven't been able to find all this information gathered in one place, so I've worked a few
things out for myself by experiment and calculation.
I would be glad to hear from anyone with corrections.
(1) The eye's response to light is logarithmic.
The human eye responds to light in terms of equal ratios rather than
equal increments - that is,
in terms of multiplication rather than addition.
Another way to say this is that the eye's response is logarithmic.
What I mean by this is that if I ask you adjust several lights to arrange
their brightness in equal steps, you'll probably give them actual brightnesses
of something like 10, 20, 40, 80, 160, or maybe 10, 30, 90, 270, 810,
not 100, 200, 300, 400 or 100, 150, 200, 250.
That is, each step will multiply the previous step by a constant.
We call this logarithmic because the logarithms of the values
are arranged in equal steps.
Take our hypothetical series 10, 20, 40, 80, 160, and take the logarithms
to base 10. They come out to 1.0, 1.3, 1.6, 1.9, and 2.2. That is,
when you double the actual value, you're adding 0.3 (more precisely 0.301)
to its logarithm.
That's handy, because logarithms let you substitute addition (or shifting along a scale)
for multiplication (expanding or contracting the whole scale).
That's exactly what the eye does with light levels:
we see equal steps where the physical reality is multiplication by equal constants.
(2) In film photography, we always use logarithmic scales.
Here is the kind of characteristic curve you'll find on a film data sheet:
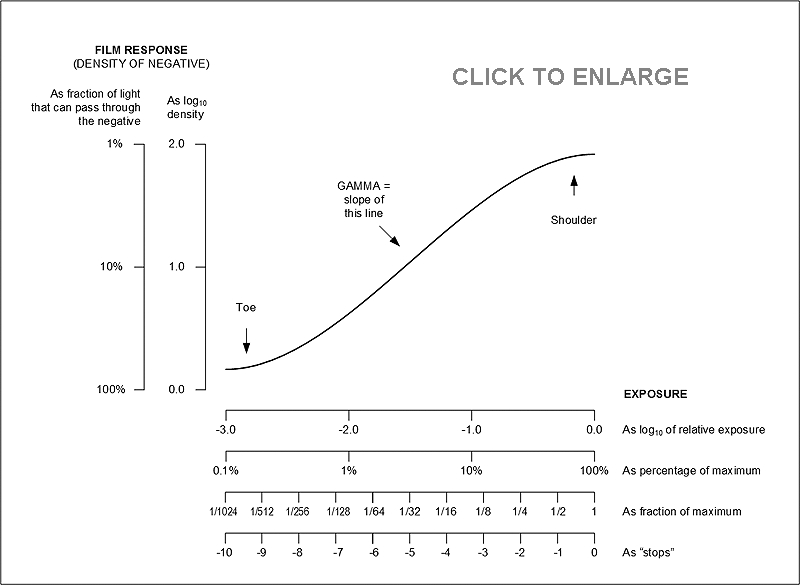
Notice that the are logarithmic.
Equal distances represent equal ratios.
Each scale is labeled several ways, all equivalent.
An ideal film would have a straight "curve" - would produce density proportional to exposure.
Or would that really be ideal?
Actually, some compression at the toe helps get rid of lens flare,
and compression at the shoulder helps deal with overexposed pictures.
As we'll see, digital cameras imitate this.
The gamma of a film negative is the slope of the straight-line portion of the curve.
Typically, negatives have a gamma of about 0.7 and are printed on photographic paper
with a gamma of about 1.4 (to turn the negative back into a positive). Note that 0.7×1.4=1.0,
so the picture looks like the original.
(3) The computer screen's response to pixel values is close to antilogarithmic.
Digital pictures don't have negatives.
Instead, they are stored as enormous grids of pixels each of which has a value from 0 to 255
(actually, three such values, for red, green, and blue, but for now, we'll think in black and white).
These are 8-bit pixels;
you may also encounter 12-bit pixels (0 to 4095) and 16-bit pixels (0 to 65,535).
How do pixel values map onto the brightness of the screen?
Not linearly.
In fact, the mapping is close to antilogarithmic,
so that
you can treat pixel values as a logarithmic scale for brightness.
That is, pixel values 0 to 255 look equally spaced to the human eye,
and they would be evenly spaced along the vertical scale of the graph:
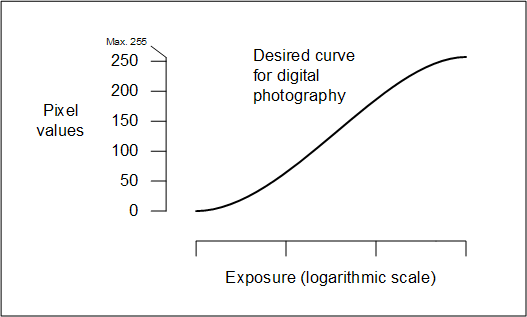
The truth of the matter is a little more complicated.
The mapping of pixel values to brightness is actually a power law,
not an antilogarithmic (exponential) function.
Specifically,
Brightness = Max brightness × (Pixel value / Max pixel value)Gamma
where
Gamma ranges from about 1.8 to 2.2, depending on how the screen is calibrated.
In conventional television technology it was 2.5, but on computers, we've brought it
down to 1.8 to match the original Apple Laserwriter, which set a lot of standards
for the digital darkroom.
This can be extremely close to the desired antilogarithmic function, especially if your
screen's black value isn't pitch-black (a common situation on CRTs).
Here's a graph that shows you just how close they can get.
The red curve represents a screen with gamma of 1.8 and a minimum black of 15% of full brightness.
The green curve is antilogarithmic.
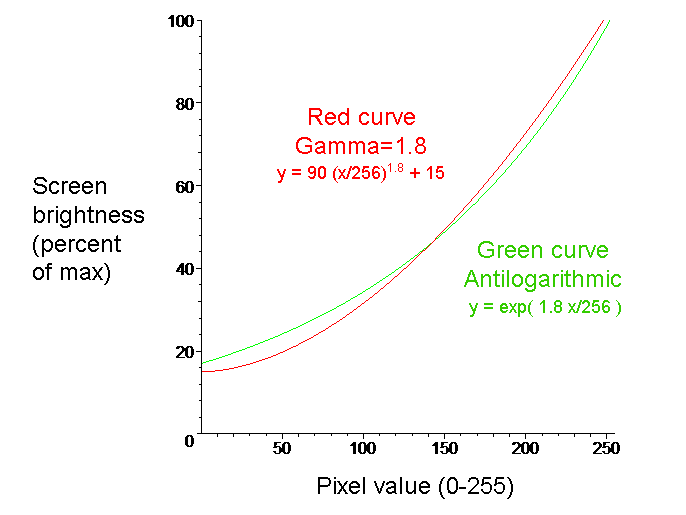
In real life, most computer screens are a bit dark in the shadows, but otherwise close
to antilogarithmic.
Screen gamma is distantly related to film gamma - but only distantly.
The two are not directly comparable.
(4) In Photoshop, the tone curves represent pixel values.
When you adjust the tone curve in Photoshop (Ctrl-M), you're editing a graph both of whose axes
are linear scales of pixel values (corresponding roughly to logarithmic scales of
brightness).
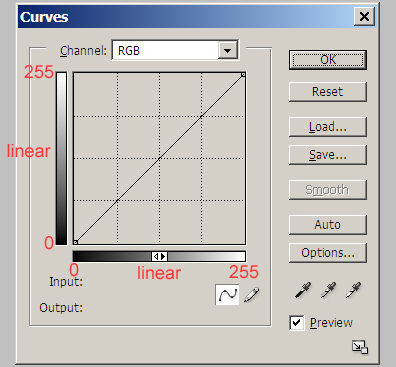
Thus, the curve does what you expect, and a straight line represents no change.
Photoshop Elements lacks the Curves adjustment, but it has Levels (Ctrl-L), and the middle
slider (shown here in red) makes the middle of the curve bend up or down. The other sliders
set the ends of the curve on the horizontal and vertical axes.
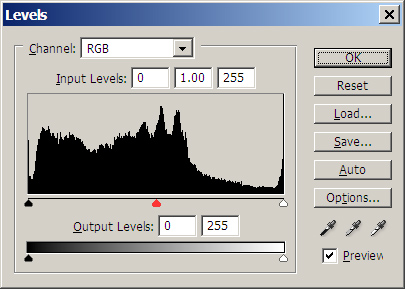
The black hump shape is a histogram that shows you how much of the picture is at each
brightness level.
This one indicates a picture most of whose surface area is darker than halfway along the scale.
(5) The digital sensor's response to light is linear.
The actual output voltage from each cell of an image sensor,
whether CCD or CMOS,
is proportional to the number of photons that struck
it during the exposure.
This means digital image sensors are ruthlessly linear, which is what makes
them so appealing for scientific use.
You can add the light from two sources and be sure that what you get is the exact sum.
You can then subtract one of them and be left with just the other.
With film, this isn't possible because the response isn't linear; 2 + 2 does not equal 4.
(6) Digital cameras normally convert sensor values to appropriate screen pixel values.
As you might expect, almost all digital cameras perform gamma correction (tone curve correction)
to make the pictures look right on an approximately antilogarithmic screen display.
Mainly, what they have to do is lighten the midtones a lot. Here's
a typical conversion function, plotted with both linear and logarithmic
scales for the sensor output:
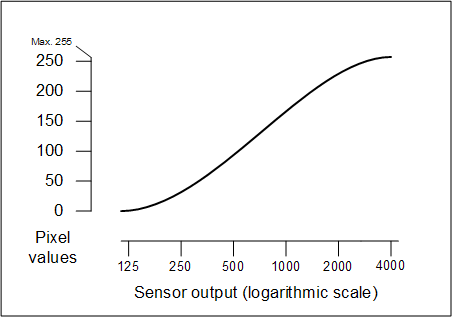
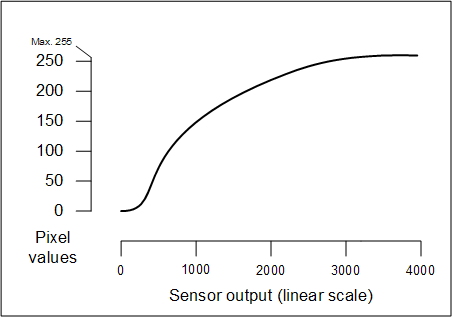
For concreteness I'm assuming a sensor with a 12-bit ADC (analog-to-digital converter)
such as the Canon Digital Rebel, with sensor outputs ranging from 0 to 4095.
The actual output of the sensor is an analog voltage.
(7) For dark frame subtraction and other kinds of analysis, we need linear conversion.
For some purposes we need to know the actual numbers that came out of the image sensor,
or numbers linearly proportional to them, without gamma correction.
This enables us to do such things as measure the brightness of objects in the picture
(important in astronomy) or subtract light from a known, unwelcome source leaving behind
only the light we actually wanted.
Related to the latter is dark frame subtraction, where we make two exposures,
one with the lenscap on, and subtract them, so that the noise from hot pixels can be
removed from the picture.
Linear image conversion (from the raw data file produced by the camera) can be done by Canon
File Viewer Utility, Canon Digital Photo Pro, ImagesPlus, and a number of other software packages. The
linear conversion function is a straight line if you use a linear scale for the sensor output;
otherwise it's quite bent. Here it is, superimposed on the graphs you just saw:
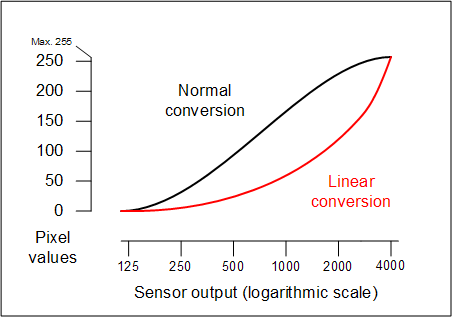
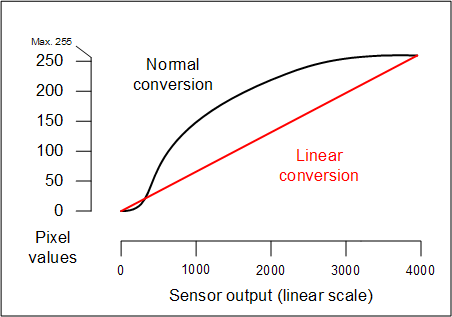
That is why, when you ask for a linear conversion in Canon Digital Photo Pro,
you see a curve that sags severely in the middle!
Copyright 2004 Michael A. Covington. Caching in search engines is explicitly permitted.
Please link to this page rather than reproducing copies of it.
This page is not in any way connected with or endorsed by any
photographic manufacturer. Many of the product names that appear
on this page are registered trademarks of their respective owners.
|









